Notes on How to Optimize GeMM
here is a note on how-to-optimize-gemm.
GeMM
GeMM is the most basic matrix multiplication kernel. It is defined as: \(C = \alpha A \times B + \beta C\)
where $A$ is $m \times k$ matrix, $B$ is $k \times n$ matrix, $C$ is $m \times n$ matrix, $\alpha$ and $\beta$ are scalars.
basic implementation is:
/* Create macros so that the matrices are stored in column-major order */
#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]
/* Routine for computing C = A * B + C */
void MY_MMult( int m, int n, int k, double *a, int lda,
double *b, int ldb,
double *c, int ldc )
{
int i, j, p;
for ( i=0; i<m; i++ ){ /* Loop over the rows of C */
for ( j=0; j<n; j++ ){ /* Loop over the columns of C */
for ( p=0; p<k; p++ ){ /* Update C( i,j ) with the inner
product of the ith row of A and
the jth column of B */
C( i,j ) = C( i,j ) + A( i,p ) * B( p,j );
}
}
}
}
where lda is the leading dimension of matrix a, ldb is the leading dimension of matrix b, ldc is the leading dimension of matrix c.
what dose leading mean? look at this class: 1.2.2 The leading dimension of a matrix youtube and 1.2.2 The leading dimension.
Note.
-
Matrix Definition:
For a matrix A, the matrix size is m×n. We use the notation $a_{i,j}$ to refer to the entry in the i-th row and j-th column of matrix A. -
Column-Major Order:
Suppose that A is column-major ordered. The index in memory when accessing a matrix is given by: j×m+i. We defined a macro:#define A(i,j) a[ (j)*m + (i) ]
This macro translates the row and column indices i and j into the corresponding memory location. -
Working with Submatrices:
We typically want to work with submatrices of larger matrices. This means that matrix A is often embedded in a much larger matrix.
In the programming language Fortran, you should provide the leading dimension of A, denoted as ldA, which represents the number of rows in the larger matrix. To index into the submatrix, we can use the formula: j×ldA+i . The leading dimension is crucial because it accounts for how many entries you need to skip in memory to move from one row to the next in the larger matrix. This ensures that we correctly access the elements of the submatrix.
Computing four elements at a time
Optimizations one: Hiding computation in a subroutine
In total, there are three nested for loops. We first rearranged the order of the outer two for loops and moved the innermost for loop into a subroutine. Now, the outer loop iterates over the columns of matrix C, while the inner loop iterates over the rows of matrix C.
I believe this change is due to the column-major order, which allows us to access entries of matrix C in contiguous memory, thus making the process faster.
/* Create macros so that the matrices are stored in column-major order */
#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]
/* Routine for computing C = A * B + C */
void AddDot( int, double *, int, double *, double * );
void MY_MMult( int m, int n, int k, double *a, int lda,
double *b, int ldb,
double *c, int ldc )
{
int i, j;
for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */
for ( i=0; i<m; i+=1 ){ /* Loop over the rows of C */
/* Update the C( i,j ) with the inner product of the ith row of A
and the jth column of B */
AddDot( k, &A( i,0 ), lda, &B( 0,j ), &C( i,j ) );
/* Update the C( i,j+1 ) with the inner product of the ith row of A
and the (j+1)th column of B */
AddDot( k, &A( i,0 ), lda, &B( 0,j+1 ), &C( i,j+1 ) );
/* Update the C( i,j+2 ) with the inner product of the ith row of A
and the (j+2)th column of B */
AddDot( k, &A( i,0 ), lda, &B( 0,j+2 ), &C( i,j+2 ) );
/* Update the C( i,j+3 ) with the inner product of the ith row of A
and the (j+1)th column of B */
AddDot( k, &A( i,0 ), lda, &B( 0,j+3 ), &C( i,j+3 ) );
}
}
}
/* Create macro to let X( i ) equal the ith element of x */
#define X(i) x[ (i)*incx ]
void AddDot( int k, double *x, int incx, double *y, double *gamma )
{
/* compute gamma := x' * y + gamma with vectors x and y of length n.
Here x starts at location x with increment (stride) incx and y starts at location y and has (implicit) stride of 1.
*/
int p;
for ( p=0; p<k; p++ ){
*gamma += X( p ) * y[ p ];
}
}
This does not yield better performance. I think this is because the innermost loop is still executed sequentially, and the cache performance is not improved.
Computing four elements at a time
- We compute C four elements at a time in a subroutine, AddDot1x4, which performs four inner products at a time:
for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */ for ( i=0; i<m; i+=1 ){ /* Loop over the rows of C */ /* Update the C( i,j ) with the inner product of the ith row of A and the jth column of B */ AddDot( k, &A( i,0 ), lda, &B( 0,j ), &C( i,j ) ); /* Update the C( i,j+1 ) with the inner product of the ith row of A and the (j+1)th column of B */ AddDot( k, &A( i,0 ), lda, &B( 0,j+1 ), &C( i,j+1 ) ); /* Update the C( i,j+2 ) with the inner product of the ith row of A and the (j+2)th column of B */ AddDot( k, &A( i,0 ), lda, &B( 0,j+2 ), &C( i,j+2 ) ); /* Update the C( i,j+3 ) with the inner product of the ith row of A and the (j+1)th column of B */ AddDot( k, &A( i,0 ), lda, &B( 0,j+3 ), &C( i,j+3 ) ); } }note: Loop Unrolling
- Now we inline the four separate inner products and fuse the loops into one, thereby computing the four inner products simultaneously in one loop
for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */
for ( i=0; i<m; i+=1 ){ /* Loop over the rows of C */
/* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in
one routine (four inner products) */
AddDot1x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
}
}
void AddDot1x4( int k, double *a, int lda, double *b, int ldb, double *c, int ldc )
{
/* So, this routine computes four elements of C:
C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ).
Notice that this routine is called with c = C( i, j ) in the
previous routine, so these are actually the elements
C( i, j ), C( i, j+1 ), C( i, j+2 ), C( i, j+3 )
in the original matrix C.
In this version, we merge the four loops, computing four inner
products simultaneously. */
int p;
for ( p=0; p<k; p++ ){
C( 0, 0 ) += A( 0, p ) * B( p, 0 );
C( 0, 1 ) += A( 0, p ) * B( p, 1 );
C( 0, 2 ) += A( 0, p ) * B( p, 2 );
C( 0, 3 ) += A( 0, p ) * B( p, 3 );
}
}
At this point, we are starting to see some performance improvements.
registers
At this point, we are starting to see some performance improvements.
Registers are faster to access than memory, so the variables that are most frequently used in a C program can be placed in registers using the register keyword.
In the previous code, we notice that within the for loop, the variables C(0, 0), C(0, 1), C(0, 2), C(0, 3), and A(0, p) are used in every iteration. If we can load these variables into registers, we can save time by avoiding repeated loading from memory. Additionally, placing the element A(p, 0) in a register can help reduce traffic between the cache and registers.
void AddDot1x4( int k, double *a, int lda, double *b, int ldb, double *c, int ldc )
{
/* So, this routine computes four elements of C:
C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ).
Notice that this routine is called with c = C( i, j ) in the
previous routine, so these are actually the elements
C( i, j ), C( i, j+1 ), C( i, j+2 ), C( i, j+3 )
in the original matrix C.
In this version, we accumulate in registers and put A( 0, p ) in a register */
int p;
register double
/* hold contributions to
C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ) */
c_00_reg, c_01_reg, c_02_reg, c_03_reg,
/* holds A( 0, p ) */
a_0p_reg;
c_00_reg = 0.0;
c_01_reg = 0.0;
c_02_reg = 0.0;
c_03_reg = 0.0;
for ( p=0; p<k; p++ ){
a_0p_reg = A( 0, p );
c_00_reg += a_0p_reg * B( p, 0 );
c_01_reg += a_0p_reg * B( p, 1 );
c_02_reg += a_0p_reg * B( p, 2 );
c_03_reg += a_0p_reg * B( p, 3 );
}
C( 0, 0 ) += c_00_reg;
C( 0, 1 ) += c_01_reg;
C( 0, 2 ) += c_02_reg;
C( 0, 3 ) += c_03_reg;
}
pointer optimize
We can further optimize the code by using pointers instead of array indexing. This change can reduce the number of memory accesses and improve performance.
In the previous code, we access B(i,j) by calculating the index i×ldb+j, which requires 2 arithmetic operations. We notice that in each iteration, we access contiguous elements of B(p,0) with an increment of p. Therefore, we can use a pointer to point to the current element of B(p,0) and then increment the pointer in each iteration.
First, we obtain pointers to the four columns of B outside the loop:
double
*b_p0_ptr = &B(0, 0),
*b_p1_ptr = &B(0, 1),
*b_p2_ptr = &B(0, 2),
*b_p3_ptr = &B(0, 3);
Since each iteration accesses the next row’s four adjacent elements, the indexing for B can be written as:
for (...) {
(*(b_p0_ptr++));
(*(b_p1_ptr++));
(*(b_p2_ptr++));
(*(b_p3_ptr++));
}
We now use four pointers, bp0_pntr, bp1_pntr, bp2_pntr, and bp3_pntr, to access the elements B( p, 0 ), B( p, 1 ), B( p, 2 ), B( p, 3 ). This reduces indexing overhead.
Indirect Addressing
- We unroll the loop by four (a relatively arbitrary choice of unrolling factor).
- We use indirect addressing to reduce the number of times the pointers need to be updated
We now use something called ‘indirect addressing’. Notice, for example, the line
```c_00_reg += a_0p_reg * *(bp0_pntr+1);``` Here
a0p_reg holds the element A( 0, p+1 ) (yes, this is a bit confusing. A better name for the variable would be good…)
We want to bp0_pntr points to element B( p, 0 ). Hence bp0_pntr+1 addresses the element B( p+1, 0 ). There is a special machine instruction to then access the element at bp0_pntr+1 that does not require the pointer to be updated.
As a result, the pointers that address the elements in the columns of B only need to be updated once every fourth iteration of the loop.
The complete code is as follows:
/* Create macros so that the matrices are stored in column-major order */
#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]
/* Routine for computing C = A * B + C */
void AddDot1x4( int, double *, int, double *, int, double *, int )
void MY_MMult( int m, int n, int k, double *a, int lda,
double *b, int ldb,
double *c, int ldc )
{
int i, j;
for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */
for ( i=0; i<m; i+=1 ){ /* Loop over the rows of C */
/* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in
one routine (four inner products) */
AddDot1x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
}
}
}
void AddDot1x4( int k, double *a, int lda, double *b, int ldb, double *c, int ldc )
{
/* So, this routine computes four elements of C:
C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ).
Notice that this routine is called with c = C( i, j ) in the
previous routine, so these are actually the elements
C( i, j ), C( i, j+1 ), C( i, j+2 ), C( i, j+3 )
in the original matrix C.
We next use indirect addressing */
int p;
register double
/* hold contributions to
C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ) */
c_00_reg, c_01_reg, c_02_reg, c_03_reg,
/* holds A( 0, p ) */
a_0p_reg;
double
/* Point to the current elements in the four columns of B */
*bp0_pntr, *bp1_pntr, *bp2_pntr, *bp3_pntr;
bp0_pntr = &B( 0, 0 );
bp1_pntr = &B( 0, 1 );
bp2_pntr = &B( 0, 2 );
bp3_pntr = &B( 0, 3 );
c_00_reg = 0.0;
c_01_reg = 0.0;
c_02_reg = 0.0;
c_03_reg = 0.0;
for ( p=0; p<k; p+=4 ){
a_0p_reg = A( 0, p );
c_00_reg += a_0p_reg * *bp0_pntr;
c_01_reg += a_0p_reg * *bp1_pntr;
c_02_reg += a_0p_reg * *bp2_pntr;
c_03_reg += a_0p_reg * *bp3_pntr;
a_0p_reg = A( 0, p+1 );
c_00_reg += a_0p_reg * *(bp0_pntr+1);
c_01_reg += a_0p_reg * *(bp1_pntr+1);
c_02_reg += a_0p_reg * *(bp2_pntr+1);
c_03_reg += a_0p_reg * *(bp3_pntr+1);
a_0p_reg = A( 0, p+2 );
c_00_reg += a_0p_reg * *(bp0_pntr+2);
c_01_reg += a_0p_reg * *(bp1_pntr+2);
c_02_reg += a_0p_reg * *(bp2_pntr+2);
c_03_reg += a_0p_reg * *(bp3_pntr+2);
a_0p_reg = A( 0, p+3 );
c_00_reg += a_0p_reg * *(bp0_pntr+3);
c_01_reg += a_0p_reg * *(bp1_pntr+3);
c_02_reg += a_0p_reg * *(bp2_pntr+3);
c_03_reg += a_0p_reg * *(bp3_pntr+3);
bp0_pntr+=4;
bp1_pntr+=4;
bp2_pntr+=4;
bp3_pntr+=4;
}
C( 0, 0 ) += c_00_reg;
C( 0, 1 ) += c_01_reg;
C( 0, 2 ) += c_02_reg;
C( 0, 3 ) += c_03_reg;
}
Computing a 4 x 4 Block of C at a Time
In contrast to the previous algorithm, this method computes a 4 x 4 block of C in a single operation. We declare fourteen register variables—c_00_reg, c_01_reg, and so on—to store the results of the fourteen elements of C. This algorithm calculates the entire 4 x 4 block by executing the previously described solution for a 1 x 4 block of C four times. The remaining parts of the algorithm are unchanged from the previous description.
/* Create macros so that the matrices are stored in column-major order */
#define A(i,j) a[ (j)*lda + (i) ]
#define B(i,j) b[ (j)*ldb + (i) ]
#define C(i,j) c[ (j)*ldc + (i) ]
/* Routine for computing C = A * B + C */
void AddDot4x4( int, double *, int, double *, int, double *, int );
void MY_MMult( int m, int n, int k, double *a, int lda,
double *b, int ldb,
double *c, int ldc )
{
int i, j;
for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */
for ( i=0; i<m; i+=4 ){ /* Loop over the rows of C */
/* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in
one routine (four inner products) */
AddDot4x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc );
}
}
}
void AddDot4x4( int k, double *a, int lda, double *b, int ldb, double *c, int ldc )
{
/* So, this routine computes a 4x4 block of matrix A
C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ).
C( 1, 0 ), C( 1, 1 ), C( 1, 2 ), C( 1, 3 ).
C( 2, 0 ), C( 2, 1 ), C( 2, 2 ), C( 2, 3 ).
C( 3, 0 ), C( 3, 1 ), C( 3, 2 ), C( 3, 3 ).
Notice that this routine is called with c = C( i, j ) in the
previous routine, so these are actually the elements
C( i , j ), C( i , j+1 ), C( i , j+2 ), C( i , j+3 )
C( i+1, j ), C( i+1, j+1 ), C( i+1, j+2 ), C( i+1, j+3 )
C( i+2, j ), C( i+2, j+1 ), C( i+2, j+2 ), C( i+2, j+3 )
C( i+3, j ), C( i+3, j+1 ), C( i+3, j+2 ), C( i+3, j+3 )
in the original matrix C
In this version, we use registers for elements in the current row
of B as well */
int p;
register double
/* hold contributions to
C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 )
C( 1, 0 ), C( 1, 1 ), C( 1, 2 ), C( 1, 3 )
C( 2, 0 ), C( 2, 1 ), C( 2, 2 ), C( 2, 3 )
C( 3, 0 ), C( 3, 1 ), C( 3, 2 ), C( 3, 3 ) */
c_00_reg, c_01_reg, c_02_reg, c_03_reg,
c_10_reg, c_11_reg, c_12_reg, c_13_reg,
c_20_reg, c_21_reg, c_22_reg, c_23_reg,
c_30_reg, c_31_reg, c_32_reg, c_33_reg,
/* hold
A( 0, p )
A( 1, p )
A( 2, p )
A( 3, p ) */
a_0p_reg,
a_1p_reg,
a_2p_reg,
a_3p_reg,
b_p0_reg,
b_p1_reg,
b_p2_reg,
b_p3_reg;
double
/* Point to the current elements in the four columns of B */
*b_p0_pntr, *b_p1_pntr, *b_p2_pntr, *b_p3_pntr;
b_p0_pntr = &B( 0, 0 );
b_p1_pntr = &B( 0, 1 );
b_p2_pntr = &B( 0, 2 );
b_p3_pntr = &B( 0, 3 );
c_00_reg = 0.0; c_01_reg = 0.0; c_02_reg = 0.0; c_03_reg = 0.0;
c_10_reg = 0.0; c_11_reg = 0.0; c_12_reg = 0.0; c_13_reg = 0.0;
c_20_reg = 0.0; c_21_reg = 0.0; c_22_reg = 0.0; c_23_reg = 0.0;
c_30_reg = 0.0; c_31_reg = 0.0; c_32_reg = 0.0; c_33_reg = 0.0;
for ( p=0; p<k; p++ ){
a_0p_reg = A( 0, p );
a_1p_reg = A( 1, p );
a_2p_reg = A( 2, p );
a_3p_reg = A( 3, p );
b_p0_reg = *b_p0_pntr++;
b_p1_reg = *b_p1_pntr++;
b_p2_reg = *b_p2_pntr++;
b_p3_reg = *b_p3_pntr++;
/* First row */
c_00_reg += a_0p_reg * b_p0_reg;
c_01_reg += a_0p_reg * b_p1_reg;
c_02_reg += a_0p_reg * b_p2_reg;
c_03_reg += a_0p_reg * b_p3_reg;
/* Second row */
c_10_reg += a_1p_reg * b_p0_reg;
c_11_reg += a_1p_reg * b_p1_reg;
c_12_reg += a_1p_reg * b_p2_reg;
c_13_reg += a_1p_reg * b_p3_reg;
/* Third row */
c_20_reg += a_2p_reg * b_p0_reg;
c_21_reg += a_2p_reg * b_p1_reg;
c_22_reg += a_2p_reg * b_p2_reg;
c_23_reg += a_2p_reg * b_p3_reg;
/* Four row */
c_30_reg += a_3p_reg * b_p0_reg;
c_31_reg += a_3p_reg * b_p1_reg;
c_32_reg += a_3p_reg * b_p2_reg;
c_33_reg += a_3p_reg * b_p3_reg;
}
C( 0, 0 ) += c_00_reg; C( 0, 1 ) += c_01_reg; C( 0, 2 ) += c_02_reg; C( 0, 3 ) += c_03_reg;
C( 1, 0 ) += c_10_reg; C( 1, 1 ) += c_11_reg; C( 1, 2 ) += c_12_reg; C( 1, 3 ) += c_13_reg;
C( 2, 0 ) += c_20_reg; C( 2, 1 ) += c_21_reg; C( 2, 2 ) += c_22_reg; C( 2, 3 ) += c_23_reg;
C( 3, 0 ) += c_30_reg; C( 3, 1 ) += c_31_reg; C( 3, 2 ) += c_32_reg; C( 3, 3 ) += c_33_reg;
}
In this step, we are modifying the order of calculations for the register variables of C. Instead of processing each row of C sequentially, we now calculate two rows at a time. This change sets us up to take advantage of vector operations, which allows us to simultaneously update pairs of elements, specifically C(0,j) and C(1,j) (for j = 0,…,3).
/* First row and second rows */
c_00_reg += a_0p_reg * b_p0_reg;
c_10_reg += a_1p_reg * b_p0_reg;
c_01_reg += a_0p_reg * b_p1_reg;
c_11_reg += a_1p_reg * b_p1_reg;
c_02_reg += a_0p_reg * b_p2_reg;
c_12_reg += a_1p_reg * b_p2_reg;
c_03_reg += a_0p_reg * b_p3_reg;
c_13_reg += a_1p_reg * b_p3_reg;
/* Third and fourth rows */
c_20_reg += a_2p_reg * b_p0_reg;
c_30_reg += a_3p_reg * b_p0_reg;
c_21_reg += a_2p_reg * b_p1_reg;
c_31_reg += a_3p_reg * b_p1_reg;
c_22_reg += a_2p_reg * b_p2_reg;
c_32_reg += a_3p_reg * b_p2_reg;
c_23_reg += a_2p_reg * b_p3_reg;
c_33_reg += a_3p_reg * b_p3_reg;
Now, we utilize vector registers and vector operations to enhance our calculations. For instance, we can compute two elements of C simultaneously. Previously, we had:
c_00_reg += a_0p_reg * b_p0_reg;
c_10_reg += a_1p_reg * b_p0_reg;
With vectorization, we can express this as:
c_00_c_10_vreg.v += a_0p_a_1p_vreg.v * b_p0_vreg.v;
We notice a considerable performance boost.
Blocking to maintain performance
In order to maintain the performance attained for smaller problem sizes, we block matrix C (and A and B correspondingly):
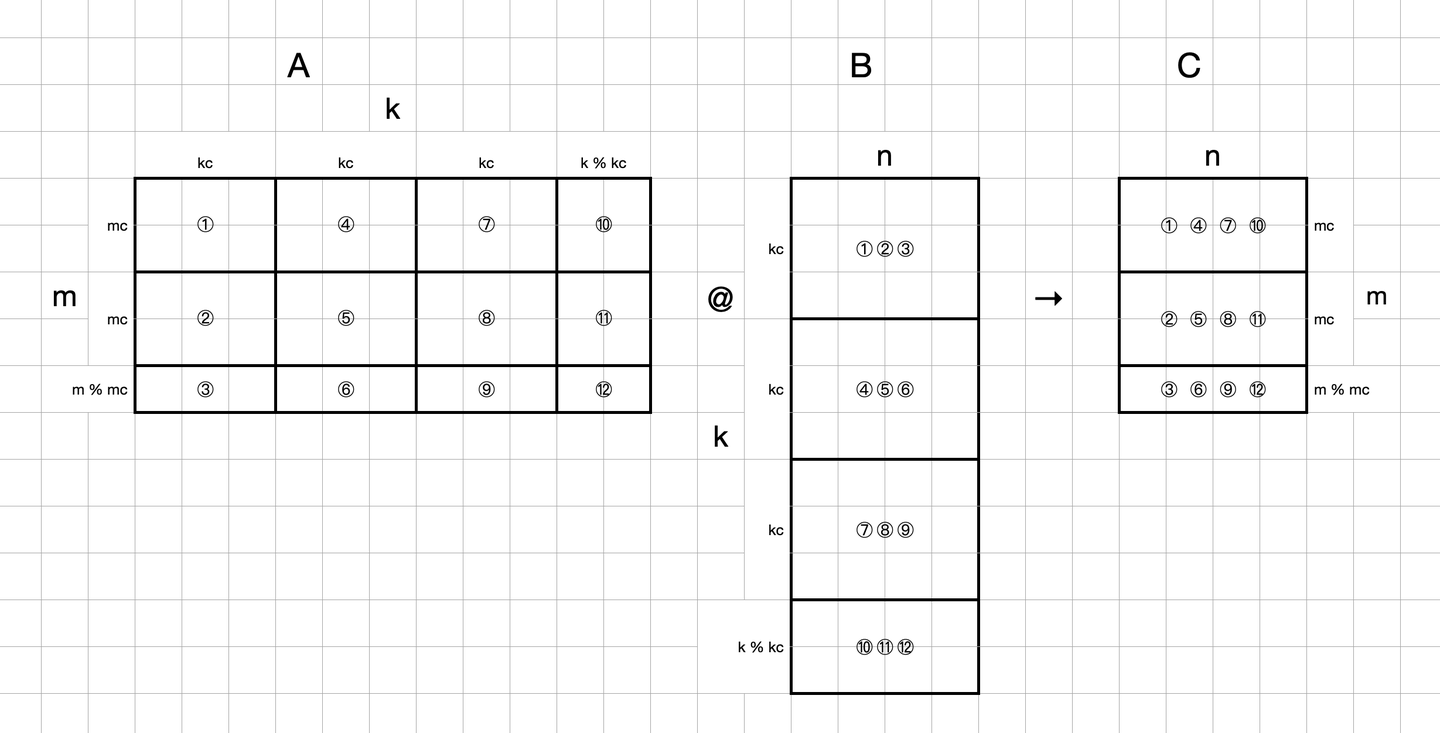
Cache Lines and Structure
modern processors have a significant number of cache lines in each level of cache. The number of cache lines depends on the size of the cache and the size of each cache line.
- Cache Line Size: Typically 64 bytes.
- Cache Levels:
- L1 Cache: Smaller, usually 32 KB, and has fewer cache lines.
- L2 Cache: Larger, typically 256 KB to 1 MB, with more cache lines.
- L3 Cache: Much larger, several MBs, with many cache lines shared among cores.
How Cache Replacement Works?
Caches use various replacement policies to decide which cache line to evict when a cache miss occurs. Common policies include:
-
Least Recently Used (LRU): Evicts the cache line that has been least recently accessed.
-
First In, First Out (FIFO): Evicts the oldest cache line in the set.
-
Random Replacement: Randomly selects a cache line to evict.
Accessing Elements of B and A
Example with Large Matrix B
Suppose matrix B is very large and stored in row-major order. When processing tiles, consider the following:
- Tile Size (BLOCK_SIZE): 3 (for simplicity).
- Sub-matrix Bsub:
1 2 3 4 5 6 7 8 9
Cache Loading Behavior
- First Column of Bsub:
- Access element
1(first element, first row). - The cache line loads elements
1,2, and3(because they are contiguous in memory).
- Access element
- Second Column of Bsub:
- Access element
4(first element, second row). - A cache miss occurs if
4is not already in the cache. - The cache loads a new cache line with elements
4,5, and6(next row).
- Access element
Elements of A
When discussing elements of A:
- Row Access of A:
- Since A is also stored in row-major order, accessing elements row-wise is cache-friendly.
- For example, accessing elements of a row in Asub (
1,2,3) will load the entire row into the cache line.
- Cache Behavior:
- When processing tiles, rows of Asub are loaded into the cache efficiently.
- Subsequent accesses to the same row do not cause cache misses, ensuring efficient reuse.
Your notes on cache misses in the provided matrix multiplication code are mostly accurate, but there are some nuances to consider. Let’s analyze the code and your observations step by step:
Matrix Multiplication Code:
void matrixMultiply(int N, double *A, double *B, double *C) {
for (int i = 0; i < N; ++i) {
for (int k = 0; k < N; ++k) {
for (int j = 0; j < N; ++j) {
C[i * N + j] += A[i * N + k] * B[k * N + j];
}
}
}
}
Assumptions:
- Matrix Size (N x N): The matrices are large, and $N \gg c$ (cache line size).
- Cache Line Size: $c$
Cache Analysis:
- Inner Loop over
j:- Accessing
A[i * N + k]: This element is accessed once per iteration of thekloop and remains constant for alljiterations. Therefore, it benefits from temporal locality, and subsequent accesses can hit in the cache. - Accessing
B[k * N + j]: This element is accessed once per iteration of thejloop. Sincejiterates over the entire row ofB, and assumingBis stored in row-major order, each access toB[k * N + j]is sequential. This sequential access pattern is cache-friendly, leading to fewer cache misses. - Accessing
C[i * N + j]: This element is accessed once per iteration of thejloop. Similar toB,Cis accessed sequentially by row, resulting in cache-friendly access patterns and reduced cache misses.
- Accessing
- Middle Loop over
k:- Accessing
A[i * N + k]: This element is accessed once per iteration of thekloop. Given thatAis stored in row-major order, accessingA[i * N + k]sequentially by row is cache-friendly, leading to fewer cache misses. - Accessing
B[k * N + j]: This element is accessed once per iteration of thejloop within eachkiteration. SinceBis accessed sequentially by column, and assumingBis stored in row-major order, this access pattern can lead to cache misses due to non-sequential access. However, ifBwere stored in column-major order, this access pattern would be cache-friendly. - Accessing
C[i * N + j]: This element is accessed once per iteration of thejloop within eachkiteration. As with the inner loop,Cis accessed sequentially by row, resulting in cache-friendly access patterns and reduced cache misses.
- Accessing
- Outer Loop over
i:- Accessing
A[i * N + k]: This element is accessed once per iteration of thekloop within eachiiteration. Given thatAis stored in row-major order, accessingA[i * N + k]sequentially by row is cache-friendly, leading to fewer cache misses. - Accessing
B[k * N + j]: This element is accessed once per iteration of thejloop within eachkiteration. As mentioned earlier, ifBis stored in row-major order, this access pattern can lead to cache misses due to non-sequential access. However, ifBwere stored in column-major order, this access pattern would be cache-friendly. - Accessing
C[i * N + j]: This element is accessed once per iteration of thejloop within eachkiteration. As with the inner and middle loops,Cis accessed sequentially by row, resulting in cache-friendly access patterns and reduced cache misses.
- Accessing
Summary:
- Total Cache Misses for
A: Given thatAis accessed sequentially by row, the cache miss rate is approximately $\frac{N}{c}$ for each iteration of thekloop. Since thekloop runs $N$ times, the total cache misses forAare approximately $N \times \frac{N}{c} = \frac{N^2}{c}$. - Total Cache Misses for
B: SinceBis accessed sequentially by column, the cache miss rate is approximately $\frac{N}{c}$ for each iteration of thejloop. Thejloop runs $N$ times, and for eachj, thekloop runs $N$ times, leading to a total of $N \times N \times \frac{N}{c} = \frac{N^3}{c}$ cache misses forB. - Total Cache Misses for
C: SinceCis accessed sequentially by row, the cache miss rate is approximately $\frac{N}{c}$ for each iteration of thejloop. Thejloop runs $N$ times, and for eachj, thekloop runs $N$ times, leading to a total of $N \times N \times \frac{N}{c} = \frac{N^3}{c}$ cache misses forC.
here is tiling code
#define BLOCK_SIZE 16
void matrixMultiplyTiled(int N, double *A, double *B, double *C) {
for (int i = 0; i < N; i += BLOCK_SIZE) {
for (int k = 0; k < N; k += BLOCK_SIZE) {
for (int j = 0; j < N; j += BLOCK_SIZE) {
// Process the tiles
for (int ii = i; ii < i + BLOCK_SIZE; ++ii) {
for (int kk = k; kk < k + BLOCK_SIZE; ++kk) {
double sum = 0.0;
for (int jj = j; jj < j + BLOCK_SIZE; ++jj){
sum += A[ii * N + kk] * B[kk * N + jj];
}
C[ii * N + jj] += sum;
}
}
}
}
}
}
- loop over jj
- For each iteration of jj, A[ii * N + kk] and sum are reused.
- Cache miss for B[kk * N + jj] is b/c.
- loop over kk
- For each iteration of kk, C[ii * N + jj] is reused.
- Cache miss for A[ii * N + kk] is b/c.
- Cache miss for B[kk * N + jj] is b.
- loop over ii
- For each iteration of ii, B[kk * N + jj] is reused.
- Cache miss for A[ii * N + kk] is b.
- Cache miss for C[ii * N + jj] is b.
suppose BLOCK_SIZE =b
Summary
- Total Cache Misses for A: b/c * N/b * N/b =$\frac{N^2}{b c}$.
- Total Cache Misses for B: $\frac{N^2}{c}$.
- Total Cache Misses for C: $\frac{N^2}{c}$.